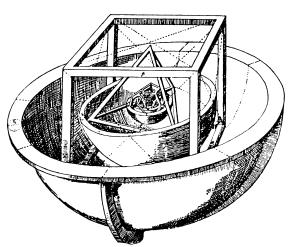
Platonische Körper in Keplers 'Harmonia mundi'
Die Mathematik zeigt sich in diesem Lehrstück von einer ihrer schönsten und "begreifbarsten" Seiten: den Platonischen Körpern.
Zunächst führt Raffaels "Schule von Athen" in die antik-philosophischen Ursprünge der Geometrie ein. Dann werden aus gleichseitigen Papp-Dreiecken, -Quadraten, -Fünfecken usw. möglichst regelmäßige Raumkörper gebildet. Siehe da: Nur fünf wirklich regelmäßige Körper sind möglich, was mit Wyss bzw. Euklid auch theoretisch begründet wird. Bei eingehender Betrachtung zum Beispiel des Würfels lassen sich erstaunliche Entdeckungen machen: Wenn man einen Tonwürfel immer weiter an den Ecken abschleift, entstehen immer wieder neue Formen: Über verschiedene Zwischenstufen wird er dann zu einem Oktaeder und offenbart geometrische Zusammenhänge, die sich bei allen fünf Körpern finden lassen. Platons Idee der Zuordnung der Körper zu den vier Elementen sowie dem Himmelskörper erweitert den Blick philosophisch; Euklid zeigt die Kugel als Mutter aller regelmäßigen Körper; Keplers Zuordnung zu den Planetenbahnen führt in den astronomischen Makrokosmos und "platonisch gewachsene" Kristallformen weisen in den mineralogischen Mikrokosmos. Am Ende steht eine Verflechtung aus fünf Wissenschaftsbereichen und eine Vitrine mit Platonischen Körpern samt Steckbriefen.